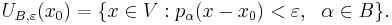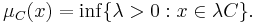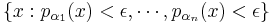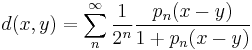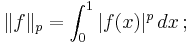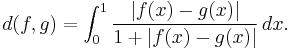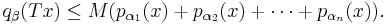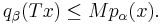Locally convex topological vector space

In functional analysis and related areas of mathematics, locally convex topological vector spaces or locally convex spaces are examples of topological vector spaces (TVS) which generalize normed spaces. They can be defined as topological vector spaces whose topology is generated by translations of balanced, absorbent, convex sets. Alternatively they can be defined as a vector space with a family of seminorms, and a topology can be defined in terms of that family. Although in general such spaces are not necessarily normable, the existence of a convex local base for the zero vector is strong enough for the Hahn–Banach theorem to hold, yielding a sufficiently rich theory of continuous linear functionals.

Fréchet spaces are locally convex spaces which are metrizable and complete with respect to this metric. They are generalizations of Banach spaces, which are complete vector spaces with respect to a norm.

1 Definition
2 Further definitions and properties
3 Examples and nonexamples
- 3.1 Examples of locally convex spaces
- 3.2 Examples of spaces lacking local convexity
4 Continuous linear mappings
5 References
6 See also

Definition

Suppose V is a vector space over K, a subfield of the complex numbers (normally C itself or R). A locally convex space is defined either in terms of convex sets, or equivalently in terms of seminorms.

Convex sets

A subset C in V is called

Convex if for each x and y in C, tx+(1–t)y is in C for all t in the unit interval, that is whenever 0 ≤ t ≤ 1. In other words, C contains all line segments between points in C.
Circled if for all x in C, λx is in C if |λ|=1. If the underlying field K is the real numbers, this means that C is equal to its reflection through the origin. For a complex vector space V, it means for any x in C, C contains the circle through x, centred on the origin, in the one-dimensional complex subspace generated by x.
A cone (when the underlying field is ordered) if for every x in C and 0 ≤ λ ≤ 1, λx is in C.
Balanced if for all x in C, λx is in C if |λ| ≤ 1. If the underlying field K is the real numbers, this means that if x is in C, C contains the line segment between x and -x. For a complex vector space V, it means for any x in C, C contains the disk with x on its boundary, centred on the origin, in the one-dimensional complex subspace generated by x. Equivalently, a balanced set is a circled cone.
Absorbent or absorbing if the union of tC over all t > 0 is all of V, or equivalently for every x in V, tx is in C for some t > 0. The set C can be scaled out to absorb every point in the space.
Absolutely convex if it is both balanced and convex.

More succinctly, a subset of V is absolutely convex if it is closed under linear combinations whose coefficients absolutely sum to ≤ 1. Such a set is absorbent if it spans all of V.

A locally convex topological vector space is a topological vector space in which the origin has a local base of absolutely convex absorbent sets. Because translation is (by definition of "topological vector space") continuous, all translations are homeomorphisms, so every base for the neighborhoods of the origin can be translated to a base for the neighborhoods of any given vector.

Seminorms

A seminorm on V is a map p : V → R such that

p is positive or positive semidefinite: p(x) ≥ 0.
p is positive homogeneous or positive scalable: p(λx) = |λ| p(x) for every scalar λ. So, in particular, p(0) = 0.
p is subadditive. It satisfies the triangle inequality: p(x + y) ≤ p(x) + p(y).

If p satisfies positive definiteness, which states that if p(x) = 0 then x = 0, then p is a norm. While in general seminorms need not be norms, there is an analogue of this criterion for families of seminorms, separatedness, defined below.

A locally convex space is then defined to be a vector space V along with a family of seminorms {p_α}_α ∈ A on V. The space carries a natural topology, the initial topology of the seminorms. In other words, it is the coarsest topology for which all mappings x → p_α(x−x₀), x₀ ∈ V, α ∈ A, are continuous. A base of neighborhoods of x₀ for this topology is obtained in the following way: for every finite subset B of A and every ε > 0, let

$U_{B, \varepsilon}(x_0) = \{x \in V�: p_\alpha(x - x_0) < \varepsilon, \ \ \alpha \in B\}.$

That the vector space operations are continuous in this topology follows from properties 2 and 3 above. The resulting TVS is locally convex because each 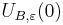$U_{B, \varepsilon}(0)$ is absolutely convex and absorbent.

Equivalence of definitions

Although the definition in terms of a neighborhood base gives a better geometric picture, the definition in terms of seminorms is easier to work with in practice. The equivalence of the two definitions follows from a construction known as the Minkowski functional or Minkowski gauge. The key feature of seminorms which ensures the convexity of their ε-balls is the triangle inequality.

For an absorbing set C such that if x is in C, then tx is in C whenever 0 ≤ t ≤ 1, define the Minkowski functional of C to be

$\mu_C(x) = \inf \{\lambda > 0: x\isin \lambda C\}.$

From this definition it follows that μ_C is a seminorm if C is balanced and convex (it is also absorbent by assumption). Conversely, given a family of seminorms, the sets

$\{x: p_{\alpha_1}(x) < \epsilon, \cdots, p_{\alpha_n}(x) < \epsilon\}$

form a base of convex absorbent balanced sets.

Further definitions and properties

A family of seminorms {p_α}_α is called total or separated or is said to separate points if whenever p_α(x) = 0 holds for every α then x is necessarily 0. A locally convex space is Hausdorff if and only if it has a separated family of seminorms. Many authors take the Hausdorff criterion in the definition.
A pseudometric is a generalisation of a metric which does not satisfy the condition that d(x,y) = 0 only when x = y. A locally convex space is pseudometrisable, meaning that its topology arises from a pseudometric, if and only if it has a countable family of seminorms. Indeed, a pseudometric inducing the same topology is then given by

$d(x,y)=\sum^\infty_n\frac{1}{2^n}\frac{p_n(x-y)}{1%2Bp_n(x-y)}$

(where the 1/2ⁿ can be replaced by any positive summable sequence a_n). This pseudometric is translation-invariant, but not homogeneous, meaning d(kx,ky) does not equal |k|d(x,y), and therefore does not define a (pseudo)norm. The pseudometric is an honest metric if and only if the family of seminorms is separated, since this is the case if and only if the space is Hausdorff. If furthermore the space is complete, the space is called a Fréchet space.
As with any topological vector space, a locally convex space is also a uniform space. Thus one may speak of uniform continuity, uniform convergence, and Cauchy sequences.
A Cauchy net in a locally convex space is a net {x_κ}_κ such that for every ε > 0 and every seminorm p_α, there exists a κ such that for every λ, μ > κ, p_α(x_λ–x_μ) < ε. In other words, the net must be Cauchy in all the seminorms simultaneously. The definition of completeness is given here in terms of nets instead of the more familiar sequences because unlike Fréchet spaces which are metrisable, general spaces may be defined by an uncountable family of pseudometrics. Sequences, which are countable by definition, cannot suffice to characterize convergence in such spaces. A locally convex space is complete if and only if every Cauchy net converges.
A family of seminorms becomes a preordered set under the relation p_α ≤ p_β if and only if there exists an M > 0 such that for all x, p_α(x) ≤ Mp_β(x). One says it is a directed family of seminorms if the family is a directed set with addition as the join, in other words if for every α and β, there is a γ such that p_α + p_β ≤ p_γ. Every family of seminorms has an equivalent directed family, meaning one which defines the same topology. Indeed, given a family {p_α}_α∈I, let Φ be the set of finite subsets of I, then for every F in Φ, define q_F=∑_α∈F p_α. One may check that {q_F}_F∈Φ is an equivalent directed family.
If the topology of the space is induced from a single seminorm, then the space is seminormable. Any locally convex space with a finite family of seminorms is seminormable. Moreover, if the space is Hausdorff (the family is separated), then the space is normable, with norm given by the sum of the seminorms. In terms of the open sets, a locally convex topological vector space is seminormable if and only if 0 has a bounded neighborhood.

Examples and nonexamples

Examples of locally convex spaces

Every normed space is a Hausdorff locally convex space, and much of the theory of locally convex spaces generalises parts of the theory of normed spaces. The family of seminorms can be taken to be the single norm. Every Banach space is a complete Hausdorff locally convex space, in particular, the L^p spaces with p ≥ 1 are locally convex.

More generally, every Fréchet space is locally convex. A Fréchet space can be defined as a complete locally convex space with a separated countable family of seminorms.

The space R^ω of real valued sequences with the family of seminorms given by 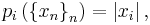$p_i \left(\left\{x_n\right\}_n\right) = \left|x_i\right|,$ i ∈ N. The countable family of seminorms is complete and separable, so this is a Fréchet space, which is not normable. Note that this is also the limit topology of the spaces Rⁿ, embedded in R^ω in the natural way, by completing finite sequences with infinitely many 0.

Given any vector space V and a collection F of linear functionals on it, V can be made into a locally convex topological vector space by giving it the weakest topology making all linear functionals in F continuous. This is known as the weak topology or the initial topology determined by F. The collection F may be the algebraic dual of V or any other collection. The family of seminorms in this case is given by p_ƒ(x) = |ƒ(x)| for all ƒ in F.

Spaces of differentiable functions give other non-normable examples. Consider the space of smooth functions ƒ : Rⁿ → C such that sup_x |x^aD^bƒ| < ∞, where a and b are multiindices. The family of seminorms define by p_a,b(ƒ) = sup_x |x^aD^bƒ(x)| is separated, and countable, and the space is complete, so this metrisable space is a Fréchet space. It is known as the Schwartz space, or the space of functions of rapid decrease, and its dual space is the space of tempered distributions.

An important function space in functional analysis is the space D(U) of smooth functions with compact support in U ⊆ Rⁿ. A more detailed construction is needed for the topology of this space because the space C^∞₀(U) is not complete in the uniform norm. The topology on D(U) is defined as follows: for any fixed compact set K ⊂ U, the space C^∞₀(K) of functions ƒ ∈ C^∞₀(U) with supp(ƒ) ⊂ K is a Fréchet space with countable family of seminorms ||ƒ||_m = sup_x |D^mƒ(x)| (these are actually bona fide norms, and the space C^∞₀(K) with the ||·||_m norm is a Banach space D^m(K)) . Given any collection {K_λ}_λ of compact sets, directed by inclusion and such that ∪_λK_λ = U, then the C^∞₀(K_λ) form a direct system, and D(U) is defined to be the limit of this system. Such a limit of Fréchet spaces is known as an LF space. More concretely, D(U) is the union of all the C^∞₀(K_λ) with the final topology which makes each inclusion map C^∞₀(K_λ)↪D(U) continuous. This space is locally convex and sequentially complete, but not complete (this means that all Cauchy sequences converge, but not necessarily more general Cauchy nets). The space is not metrisable, and so it is not a Fréchet space. The dual space of D(Rⁿ) is the space of distributions on Rⁿ.

More abstractly, given a topological space X, the space C(X) of continuous (not necessarily bounded) functions on X can be given the topology of uniform convergence on compact sets. This topology is defined by semi-norms φ_K(ƒ) = max { |ƒ(x)| : x ∈ K } (as K varies over the directed set of all compact subsets of X). When X is locally compact (e.g. an open set in Rⁿ) the Stone-Weierstrass theorem applies -- in the case of real-valued functions, any subalgebra of C(X) that separates points and contains the constant functions (e.g., the subalgebra of polynomials) is dense.

Examples of spaces lacking local convexity

Many topological vector spaces are locally convex. Examples of spaces that lack local convexity include the following:

The spaces L^p([0, 1]) for 0 < p < 1 are equipped with the F-norm

$\|f\|_p = \int_0^1 |f(x)|^p \, dx \,�;$

they are not locally convex, since the only convex neighborhood of zero is the whole space. More generally the spaces L^p(μ) with an atomless, finite measure μ and 0 < p < 1 are not locally convex.

The space of measurable functions on the unit interval [0, 1] (where we identify two functions that are equal almost everywhere) has a vector-space topology defined by the translation-invariant metric (which induces the convergence in measure of measurable functions; for random variables, convergence in measure is convergence in probability). This space is often denoted L₀.

$d(f, g) = \int_0^1 \frac{|f(x) - g(x)|}{1%2B|f(x) - g(x)|} \, dx.$

Both examples have the property that any continuous linear map to the real numbers is 0. In particular, their dual space is trivial, that is, it contains only the zero functional.

The sequence space ℓ^p, 0 < p < 1, is not locally convex.

Continuous linear mappings

Because locally convex spaces are topological spaces as well as vector spaces, the natural functions to consider between two locally convex spaces are continuous linear maps. Using the seminorms, a necessary and sufficient criterion for the continuity of a linear map can be given that closely resembles the more familiar boundedness condition found for Banach spaces.

Given locally convex spaces V and W with families of seminorms {p_α}_α and {q_β}_β respectively, a linear map T from V to W is continuous if and only if for every β there exist α₁, α₂, ... , α_n and exists an M>0 such that for all x in X

$q_\beta(Tx)\le M(p_{\alpha_1}(x) %2B p_{\alpha_2}(x)%2B\dotsb%2Bp_{\alpha_n}(x)).$

In other words, each seminorm of the range of T is bounded above by some finite sum of seminorms in the domain. If the family {p_α}_α is a directed family, and it can always be chosen to be directed as explained above, then the formula becomes even simpler and more familiar:

$q_\beta(Tx)\le Mp_\alpha(x).$

The class of all locally convex topological vector spaces forms a category with continuous linear maps as morphisms.

References

Conway, John (1990). A Course in Functional Analysis. Springer. ISBN 03-87-97245-5.
Rudin, Walter (January 1991). Functional Analysis. McGraw-Hill Science/Engineering/Math. ISBN 0-07-054236-8.